Алгоритми Гровера і Шора є важливими квантовими алгоритмами, які використовуються для розв’язання певних проблем набагато швидше, ніж це можливо на класичних комп’ютерах. Ось детальне пояснення кожного з них і їх застосування.
Алгоритм Гровера
Алгоритм Гровера — це квантовий алгоритм, який допомагає швидше знаходити елемент у невпорядкованій базі даних або просторі можливих рішень. На звичайному комп’ютері, щоб знайти потрібний елемент, необхідно перевіряти кожен запис по черзі. Якщо у нас є NNN елементів у базі, то в гіршому випадку доведеться перевірити всі NNN елементів, що займає час пропорційний NNN.
Але квантовий алгоритм Гровера значно прискорює цей процес, скорочуючи час пошуку до порядку N\sqrt{N}N. Це особливо корисно, коли кількість можливих рішень величезна, і звичайний пошук вимагає дуже багато часу.

Як це працює:
- Амплітуда ймовірностей: Квантові комп’ютери працюють з так званими кубітами, які можуть існувати одночасно в кількох станах завдяки суперпозиції. Алгоритм Гровера використовує це явище для того, щоб у процесі обчислення одночасно перевіряти кілька можливих варіантів відповіді.
- Оракул: Алгоритм використовує спеціальну функцію, яка називається “оракул”. Вона перевіряє, чи є конкретний варіант рішення правильним. Однак замість перевірки одного варіанту за один раз, алгоритм завдяки квантовим властивостям може впливати на всі можливі варіанти одночасно.
- Ітерації: Алгоритм Гровера повторює певну квантову операцію, яка збільшує ймовірність знайти правильний елемент, що й дозволяє досягти прискореного пошуку.
Застосування:
Алгоритм Гровера найчастіше застосовується для задач пошуку, наприклад:
- Знаходження ключа в криптографічній системі.
- Оптимізаційні задачі.
- Пошук у великих базах даних.
Алгоритм Шора
Алгоритм Шора – це квантовий алгоритм для факторизації великих чисел, тобто розкладу числа на прості множники. Задача факторизації є основою багатьох сучасних криптографічних систем, наприклад RSA, тому алгоритм Шора має величезне значення для криптографії.
На класичних комп’ютерах факторизація великих чисел (наприклад, чисел, що складаються з сотень або тисяч цифр) є дуже складною задачею, час розв’язання якої зростає експоненційно зі збільшенням розміру числа. Алгоритм Шора розв’язує цю задачу набагато швидше, за поліноміальний час, що робить криптосистеми на основі факторизації вразливими перед квантовими комп’ютерами.

Як це працює:
- Квантова суперпозиція: Квантові комп’ютери можуть одночасно розглядати велику кількість можливих розв’язків завдяки квантовій суперпозиції.
- Періодичність: Алгоритм Шора фактично використовує періодичні властивості чисел для того, щоб знайти найбільший спільний дільник числа, що ми намагаємось факторизувати.
- Квантове перетворення Фур’є: Одним з ключових елементів алгоритму є застосування квантового перетворення Фур’є, яке дозволяє швидко знайти період функції, що потім використовується для факторизації числа.
Застосування:
Алгоритм Шора має величезне значення для криптографії, оскільки він може зламати сучасні системи шифрування, засновані на складності факторизації великих чисел. Це викликає необхідність розробки нових криптографічних систем, стійких до квантових атак.
Алгоритм Гровера і квантовий пошук

Формально, задача пошуку, вирішувана алгоритмом Гровера, визначається функцією f(x)f(x)f(x), яка приймає значення 1 для шуканого елементу й 0 для всіх інших. Пошук зводиться до знаходження xxx, де f(x)=1f(x) = 1f(x)=1. Класичний підхід вимагає порядку O(N)O(N)O(N) запитів до функції f(x)f(x)f(x). Алгоритм Гровера, застосовуючи повторне відображення станів у гільбертовому просторі за допомогою ітерації квантової оракулярної функції та дифузійної трансформації, здатний зменшити кількість запитів до O(N)O(\sqrt{N})O(N). Це досягається через зсув амплітуд квантових станів, що відповідають правильному рішенню, завдяки багаторазовій інтерференції квантових хвиль.
Алгоритм Шора і факторизація
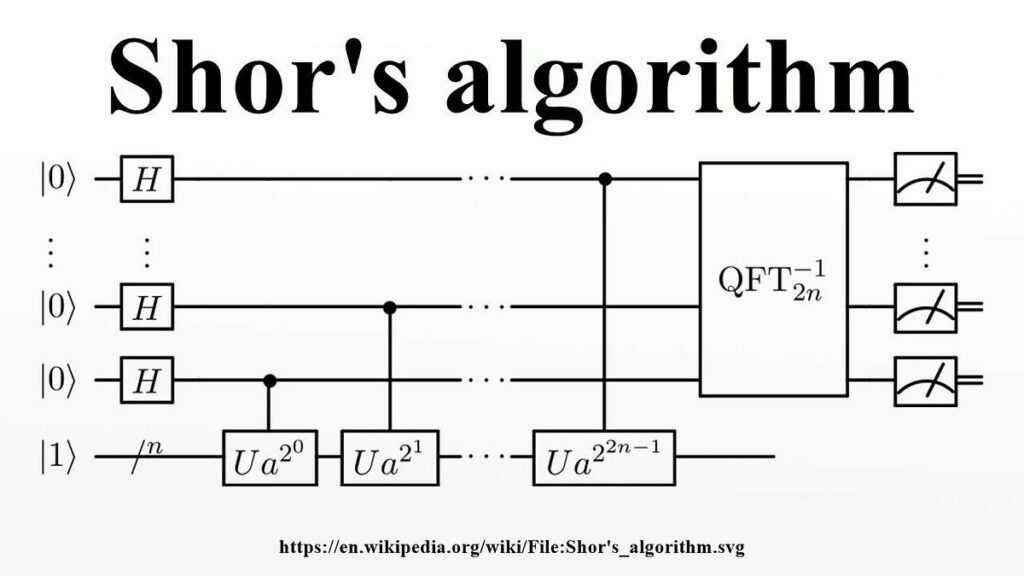
Алгоритм Шора базується на розв’язанні періодичної задачі, що еквівалентна розв’язанню проблеми факторизації. Основна ідея полягає у зведенні задачі факторизації числа NNN до пошуку періоду функції f(x)=axmod Nf(x) = a^x \mod Nf(x)=axmodN за допомогою квантового перетворення Фур’є. Завдяки суперпозиції можливих значень квантового стану й експоненційній паралельності, квантове перетворення Фур’є дозволяє визначити період rrr за поліноміальний час. Знаючи період, можна обчислити множники числа NNN за допомогою алгоритму Евкліда, що і є розв’язком задачі факторизації.
Обидва алгоритми демонструють перевагу квантових обчислень у специфічних задачах, перевершуючи класичні методи за експоненційним або поліноміальним фактором, і слугують основою для сучасних досліджень у квантовій криптографії та квантових обчисленнях.

